Expression bien parenthésée. Nous allons résoudre en Java un problème classique qui nécessite l'utilisation d'une pile. Il s'agit de vérifier qu'une chaîne de caractères contenant des parenthèses est bien parenthésée. Nous allons d'abord définir l'interface d'une pile.
/**
* Interface for a stack: a collection of objects that are inserted
* and removed according to the last-in first-out principle.
*
* @author Roberto Tamassia
* @author Michael Goodrich
* @see EmptyStackException
*/
public interface Stack {
/**
* Return the number of elements in the stack.
* @return number of elements in the stack.
*/
public int size();
/**
* Return whether the stack is empty.
* @return true if the stack is empty, false otherwise.
*/
public boolean isEmpty();
/**
* Inspect the element at the top of the stack.
* @return top element in the stack.
* @exception EmptyStackException if the stack is empty.
*/
public Object top()
throws EmptyStackException;
/**
* Insert an element at the top of the stack.
* @param element element to be inserted.
*/
public void push (Object element);
/**
* Remove the top element from the stack.
* @return element removed.
* @exception EmptyStackException if the stack is empty.
*/
public Object pop()
throws EmptyStackException;
}
Cette interface définit le type des opérations d'une pile. Notez que
l'on mentionne le type d'exceptions EmptyStackException,
dont la classe est donnée ci-dessous. Cette classe ne comporte qu'un
constructeur, qui fait lui-même appel au constructeur de la classe
parente.
/**
* Runtime exception thrown when one tries to perform operation top or
* pop on an empty stack.
*/
public class EmptyStackException extends RuntimeException {
public EmptyStackException(String err) {
super(err);
}
}
Vous allez écrire la classe NodeStack, qui implémentera une
pile sous forme d'une liste chaînée. Votre classe utilisera des objets
de la classe Node. Un objet Node est une
paire constituée d'un élément et d'un Node suivant. Cet
objet est très similaire à une paire H|T en Oz. La
classe Node définit des méthodes accesseur et
modifieurs pour accéder aux éléments de la paire.
public class Node {
// Instance variables:
private Object element;
private Node next;
/** Creates a node with null references to its element and next node. */
public Node() {
this(null, null);
}
/** Creates a node with the given element and next node. */
public Node(Object e, Node n) {
element = e;
next = n;
}
// Accessor methods:
public Object getElement() {
return element;
}
public Node getNext() {
return next;
}
// Modifier methods:
public void setElement(Object newElem) {
element = newElem;
}
public void setNext(Node newNext) {
next = newNext;
}
}
Ecrivez maintenant la classe NodeStack. Pour vous aider,
nous vous donnons le squelette de la classe. Nous avons défini deux
attributs utiles. A vous de compléter le code. N'oubliez pas de vous
conformer a l'interface Stack.
public class NodeStack implements Stack {
protected Node top; // reference to the head node
protected int size; // number of elements in the stack
public NodeStack() { // constructs an empty stack
}
public int size() {
}
public boolean isEmpty() {
}
public void push(Object elem) {
}
public Object top() throws EmptyStackException {
}
public Object pop() throws EmptyStackException {
}
}
Nous pouvons maintenant résoudre le problème avec une pile. L'algorithme est très simple: on parcourt la chaîne caractère par caractère. Quand on rencontre une parenthèse ouvrante, on la met sur la pile. Quand on rencontre une parenthèse fermante, on enlève la parenthèse ouvrante au sommet de la pile et on vérifie qu'elle correspond. Si la chaîne est bien parenthésée, la pile doit être vide à la fin.
Voici le programme. Il lit des chaînes de caractères à l'entrée standard, ligne par ligne, et teste si elles sont bien parenthésées. Nous avons implémenté l'essentiel de l'algorithme. Lisez-le et complétez là où cela s'avère nécessaire.
import java.io.*;
public class ParenChecker {
/**
* renvoie true ssi s est bien parenthesee
*/
public static boolean checkParen(String s) {
Stack stack = // COMPLETEZ: creer une pile vide
for (int i = 0; i < s.length(); i++) {
switch (s.charAt(i)) {
case '(':
case '[':
case '{':
// COMPLETEZ: on met la parenthese ouvrante sur la pile
// Attention, s.charAt(i) est un char. Pour mettre un
// Object sur la pile, il faut le convertir en Character.
break;
case ')':
case ']':
case '}':
// on verifie que le sommet de la pile contient la
// parenthese ouvrante correspondante
if (stack.isEmpty()) return false;
Character c = (Character) stack.pop();
if (!match(c.charValue(), s.charAt(i))) return false;
break;
default:
break;
}
}
// COMPLETEZ: s'il reste quelque chose sur la pile, alors il
// manque des parentheses
return
}
/**
* renvoie true ssi lpar et rpar sont des parentheses ouvrante et
* fermante se correspondant
*/
public static boolean match(char lpar, char rpar) {
switch (lpar) {
case '(': return rpar == ')';
case '[': return rpar == ']';
case '{': return rpar == '}';
default: return false;
}
}
/**
* programme principal
*/
public static void main(String[] args) throws IOException {
BufferedReader stdr; // pour lire a l'entree standard
stdr = new BufferedReader(new InputStreamReader(System.in));
String line = stdr.readLine(); // premiere ligne
while (line != null) {
if (checkParen(line))
System.out.println("well parenthesized");
else
System.out.println("parenthesis mismatch");
line = stdr.readLine(); // ligne suivante
}
}
}
Inversion d'une chaîne de caractères.
Réutilisez la pile de l'exercice précédent pour inverser une chaîne de
caractères, c'est-à-dire la présenter du dernier au premier caractères.
L'algorithme est le suivant. Prenez les caractères de la chaîne du
premier au dernier, et mettez-les sur la pile. Ensuite, retirez les
caractères de la pile, et ajoutez chacun à la fin d'une chaîne
initialement vide. Notez que l'opérateur "+" permet de
concaténer des chaînes en Java.
String s = "abc" + "def"; // construit la chaine "abcdef"
Le problème de Josephus. Ce problème est inspiré d'une histoire attribuée à Josephus Flavius:
Josephus Flavius était un historien juif célèbre du premier siècle. Pendant la guerre juive-romaine, il a été pris au piège dans une caverne avec un groupe de 40 soldats cernés par des Romains. La légende dit que, préférant la mort à la capture, les Juifs décidèrent de former un cercle et de tuer la troisième personne vivante rencontrée en suivant le parcours autour du cercle, et ceci jusqu'à ce qu'il ne reste qu'une personne : cette personne devant alors se suicider. Josephus, peu enthousiaste à l'idée de mourir, trouva rapidement la bonne place dans le cercle afin de rester en vie.On généralise le problème en considérant n éléments disposés en cercle, et le processus élimine chaque m-ième élément dans un parcours autour du cercle. Le but est de déterminer quel est le dernier élément.
On peut résoudre ce problème en utilisant une file. Une file est une séquence où les éléments sont insérés d'un côté (l'arrière) et retirés de l'autre (l'avant). Les éléments sont donc retirés dans l'ordre où ils sont insérés dans la file.
Le problème se résoud de la façon suivante. On commence par mettre tous les éléments dans la file. Ensuite, on retire m éléments de la file. Chaque élément retiré est immédiatement réinséré dans la file, à l'exception du m-ième. On continue ce processus jusqu'à ce qu'il n'y ait plus qu'un seul élément dans la file.
Vous allez implémenter une file, dont l'interface est définie
ci-dessous. La classe EmptyQueueException est définie de
façon similaire à EmptyStackException dans l'exercice 1.
public interface Queue {
/**
* Returns the number of elements in the queue.
* @return number of elements in the queue.
*/
public int size();
/**
* Returns whether the queue is empty.
* @return true if the queue is empty, false otherwise.
*/
public boolean isEmpty();
/**
* Inspects the element at the front of the queue.
* @return element at the front of the queue.
* @exception EmptyQueueException if the queue is empty.
*/
public Object front() throws EmptyQueueException;
/**
* Inserts an element at the rear of the queue.
* @param element new element to be inserted.
*/
public void enqueue (Object element);
/**
* Removes the element at the front of the queue.
* @return element removed.
* @exception EmptyQueueException if the queue is empty.
*/
public Object dequeue() throws EmptyQueueException;
}
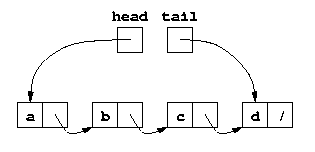
Implémentez la classe NodeQueue. Cette classe utilise les
objets Node de l'exercice 1. La classe a au moins deux
attributs de type Node. L'attribut head est
le noeud contenant le premier élément à retirer de la file, tandis que
tail est le noeud contenant le dernier élément inséré. Le
schéma suivant illustre cela dans le cas d'une file dans laquelle on a
inséré les éléments a, b, c et
d. Faites un schéma similaire pour une file vide.
Ecrivez ensuite un programme qui résoud le problème. Le programme doit donner la position de l'élément restant, en convenant que les éléments sont numérotés de 1 à n.