Séance 2
Programmation récursive avec des entiers

L'objectif de cette séance est de se familiariser avec les fonctions et procédures récursives.

Enoncés des exercices

  1. Nombres triangulaires. Écrivez une fonction récursive Sum qui calcule la somme des n premiers nombres entiers, en commençant par 1. Par exemple, {Sum 6} retourne 21 = 1+2+3+4+5+6.

  2. Miroir, mon beau miroir... Il y a deux opérateurs en Oz pour faire la division des nombres entiers: div et mod.

    Écrivez une fonction récursive Mirror qui prend un entier positif n et renvoie les chiffres du nombre en ordre inverse. Par exemple, l'appel {Mirror 12345} retourne 54321. Considérez que n ne commence ni ne finit par 0 (zéro). Naturellement, div et mod sont utiles pour écrire cette fonction.

    Aide: utilisez un accumulateur. Quel est l'invariant satisfait par la fonction avec accumulateur?

  3. Univers parallèle (première partie). Dans un univers parallèle, l'un d'entre vous écrit ce code en réponse à la question 3. 

       declare
   fun {Foo N}
      if N<10 then 1
      else 1+{Foo (N div 10)}
      end
   end
    Sa réponse est correcte...

  4. Univers parallèle (deuxième partie). Une autre étudiante a répondu avec un code alternatif. Son code est le suivant. 

       declare
   local
      fun {FooHelper N Acc}
         if N<10 then Acc+1
         else {FooHelper (N div 10) Acc+1}
         end
      end
   in
      fun {Foo N}
         {FooHelper N 0}
      end
   end

  5. Test de primalité. Écrivez une fonction {Premier N} qui renvoie true si l'entier N est un nombre premier, false sinon. Considérez que N est premier s'il n'est divisible par aucun nombre k tel que 2 ≤ k < N.

  6. Fibonacci (première partie). Écrivez une fonction récursive qui calcule le n-ième nombre de Fibonacci, donné par la définition suivante.

    fib(0) = 1
    fib(1) = 1
    fib(n) = fib(n-1) + fib(n-2)     si n > 1

  7. Fibonacci (deuxième partie). Écrivez une nouvelle version de Fibonacci, où le nombre d'appels récursifs pour n est en O(n). Aide: utilisez une fonction avec un (ou plusieurs) accumulateur(s). Quel est l'invariant de cette fonction?

  8. Un, deux, trois, nous irons au bois (première partie). Une procédure est une suite d'instructions qui ne retourne pas de valeur. Par exemple, une procédure qui affiche un nombre n et son successeur peut être définie par 

       declare
   proc {BrowseNumber N}
      {Browse N}
      {Browse N+1}
   end

    Écrivez une procédure récursive CountDown qui reçoit un entier n et qui compte de n à 0, en affichant chaque nombre compté. Par exemple, {CountDown 3} va afficher 

       3
   2
   1
   0

  9. Un, deux, trois, nous irons au bois (deuxième partie). Considérez la procédure Count dont la définition est donnée ci-dessous. Lorsque cette procédure est appelée avec un entier n, elle affiche dans le browser les nombres 1 à n en ordre croissant. 

       declare
   proc {Count N}
      local
         proc {CountFrom I}
            if I=<N then {Browse I} {CountFrom I+1} end
         end
      in
         {CountFrom 1}
      end
   end
    Remarquez qu'une procédure récursive CountFrom est définie à l'intérieur du corps de la procédure Count. C'est cette procédure qui affiche les nombres dans l'ordre.

  10. Un, deux, trois, nous irons au bois (troisième partie). On veut maintenant modifier la définition de Count, afin que la définition de CountFrom se trouve à l'extérieur du corps de Count. Ainsi, ce n'est plus le corps mais la définition de Count qui dépend de CountFrom. La solution est toute simple: déplacer la déclaration de l'instruction local à l'extérieur de Count. 

       declare
   local
      proc {CountFrom I}
         if I=<N then {Browse I} {CountFrom I+1} end
      end
   in
      proc {Count N}
         {CountFrom 1}
      end
   end
    Mais le compilateur refuse cette définition!

Exercices supplémentaires

  1. Diviseurs et multiples. En arithmétique, on utilise fréquemment le plus grand commun diviseur entre deux nombres entiers. On peut le définir comme une fonction pgcd à deux variables entières qui satisfait les propriétés

    pgcd(m, n) = pgcd(n, m)
    pgcd(m, n) = pgcd(m+n, n)
    pgcd(m, m) = m
    De la seconde propriété, on peut dériver
    pgcd(m, n) = pgcd(r, n),     où r est le reste de la division de m par n.
    Implémentez une fonction PGCD en Oz, en utilisant ces propriétés. Cette fonction prend deux paramètres entiers. Aide: Sous quelle(s) condition(s) la propriété dérivée est-elle utile, c'est-à-dire r ≠ m ?

    Implémentez une fonction PPCM prenant deux paramètres entiers et renvoyant leur plus petit commun multiple. Réutilisez votre fonction PGCD.

  2. Numérotation des points du plan. Il existe une technique relativement simple pour affecter un entier naturel à chaque couple d'entiers naturels (x, y). La figure suivante illustre la technique, qui consiste à numéroter les diagonales successives du quart de plan. Les numéros des points sont en bleu.

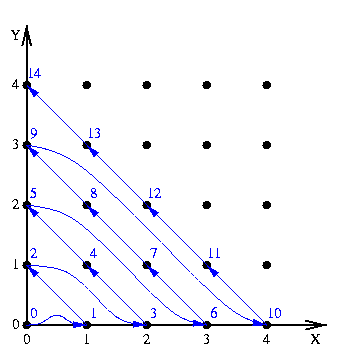
    Numérotation des points du plan

    Ecrivez une fonction Numero, prenant en paramètre deux naturels x et y, et renvoyant leur numéro suivant la technique illustrée ci-dessus. Nous proposons deux techniques.

  3. Sous les pavés... Un paveur philosophe se pose un jour la question suivante: ``De combien de façons puis-je paver une surface carrée de côté entier n avec des pavés carrés identiques et de côté entier?'' L'exemple ci-dessous montre les quatre pavages possibles pour n=6. De gauche à droite, on a utilisé des pavés de côté 6, 3, 2 et 1.

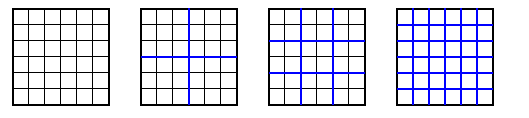
    Pavages possibles pour n=6

Boriss Mejías et Raphaël Collet - 20 septembre 2005