Moyenne des éléments d'une liste.
Ecrivez une fonction Sum qui prend en argument une liste
d'entiers et renvoie leur somme. Par convention, on peut considérer que
la liste vide a une somme nulle.
{Browse {Sum [42 17 25 61 9]}} % affiche 154
Votre fonction est-elle récursive terminale, c'est-à-dire l'appel
récursif est-il la dernière instruction ? Si ce n'est pas le cas,
tâchez de la rendre récursive terminale. Si nécessaire, définissez une
fonction auxiliaire avec un accumulateur, et spécifiez son invariant.
Définissez maintenant une fonction Average qui, appliquée à
une liste non vide d'entiers, renvoie leur moyenne. Utilisez la
division entière div. Vous pouvez réutiliser des
fonctions que vous avez déjà définies.
{Browse {Average [42 17 25 61 9]}} % affiche 30
Quelle est la complexité temporelle de votre fonction
Average ?
Mettons les listes à plat.
Écrivez une fonction Flatten prenant une liste
L en paramètre. Les éléments de L peuvent
eux-même être des listes, dont les éléments peuvent aussi être des
listes, et ainsi de suite. L'appel {Flatten L} renvoie la
liste ``aplatie'', c'est-à-dire les éléments de L et des
listes contenues dans L qui ne sont pas des listes.
Exemple:
{Browse {Flatten [a [b [c d]] e [[[f]]]]}} % affiche [a b c d e f]
Enlevons les intrus.
Écrivez une fonction FilterList telle que
{FilterList L1 L2} renvoie la liste résultant de
L1 après avoir supprimé tous les éléments qui apparaissent
dans L2. Par exemple,
{Browse {FilterList [1 2 1 4 2 3 4 5] [2 3 4]}} % affiche [1 1 5]
{Browse {FilterList [1 2 1 4 2 3 4 5] [20 2 3 4]}} % affiche [1 1 5]
{Browse {FilterList [1 2 1 4 2 3 4 5] [20 30 40]}} % affiche [1 2 1 4 2 3 4 5]
{Browse {FilterList [1 2 1 4 2 3 4 5] [1 2 3 4 5]}} % affiche nil
Il peut s'avérer utile de définir une fonction qui teste si une valeur
est élément d'une liste.
Quelle est la complexité temporelle de votre fonction ?
Je trie, tu tries, il trie...
Cet exercice consiste à implémenter des algorithmes dans le modèle
déclaratif. Les algorithmes ci-dessous sont tous des algorithmes
de tri. Vous devez donc implémenter autant de fonctions qui trient une
liste d'entiers. Chacun des algorithmes est illustré avec la liste
[5 1 7 2 6 4 3].
Pouvez-vous déterminer les complexités temporelles de ces
algorithmes ?
-
Tri par insertion. Il consiste à prendre les éléments de la liste un à un, et de les insérer au bon endroit dans une liste triée. A la fin, la seconde liste contient tous les éléments dans l'ordre. Conseil : Définissez une fonction qui calcule le résultat de l'insertion d'une valeur x dans une liste triée ys. Voir la figure gauche ci-dessous.
-
Tri par sélection. Il consiste à retirer de la liste l'élément le plus petit, le mettre dans le résultat, et de recommencer avec la liste restante. Les éléments sont donc retirés de la liste initiale exactement dans l'ordre du résultat final. Conseil : Définissez une fonction qui renvoie l'élément minimum d'une liste, ainsi qu'une fonction qui calcule le résultat de la suppression d'une valeur x d'une liste ys. Voir la figure droite ci-dessous.
Exemple de tri par insertion
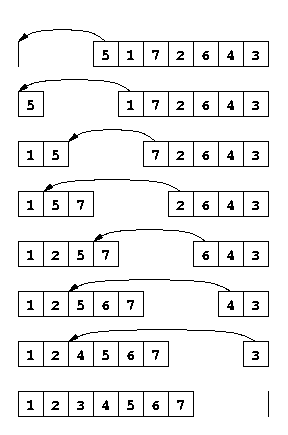
Exemple de tri par sélection
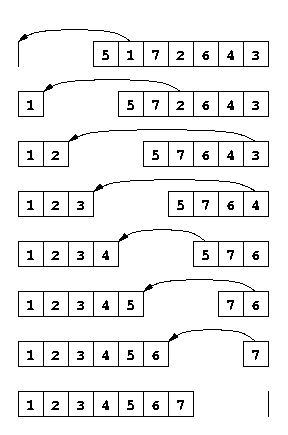
-
Tri à bulles. Il consiste à parcourir la liste en échangeant les paires d'éléments consécutifs qui ne sont pas dans l'ordre. On effectue autant de parcours que des échanges sont nécessaires. Autrement dit, on arrête dès qu'un parcours n'a fait aucun échange. Voir la figure gauche ci-dessous.
-
Tri rapide (quicksort). Cette méthode consiste à choisir une valeur pivot, et séparer les éléments de la liste en deux parties : ceux inférieurs au pivot, et ceux supérieurs au pivot. Les deux parties sont alors triées, puis concaténées (la partie inférieure avant la partie supérieure). Pour le pivot, on peut prendre le premier élément de la liste à trier. Voir la figure droite ci-dessous.
Exemple de tri à bulles
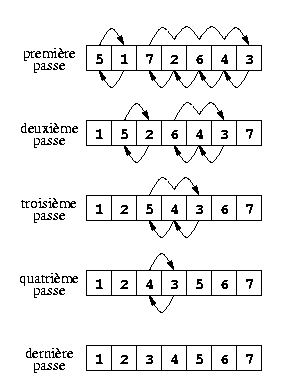
Exemple de tri rapide
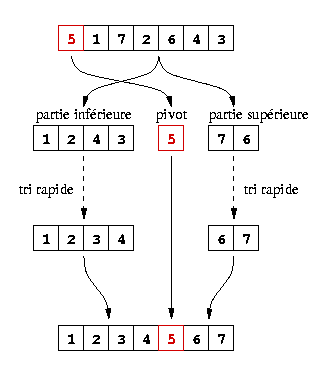
Comparaison lexicographique.
En Oz, il existe des chaînes de caractères, comme par exemple
"boris".
Une chaîne de caractères est en fait une notation pour une liste
d'entiers, chaque entier étant le code d'un caractère. Les
codes des caractères sont tels que les lettres sont dans l'ordre de leur
code (la lettre a est avant la lettre b, etc).
L'exemple ci-dessous montre la liste correspondant à
"boris".
{Browse "boris"} % affiche [98 111 114 105 115]
Ecrivez une fonction Before qui prend en argument deux
chaînes de caractères et renvoie un booléen indiquant si la première
précède la seconde dans l'ordre lexicographique, c'est-à-dire
l'ordre utilisé dans le dictionnaire.
{Browse {Before "boris" "gustavo"}} % affiche true
{Browse {Before "boris" "alberto"}} % affiche false
{Browse {Before "jean" "jeannette"}} % affiche true
Conseil: écrivez d'abord une définition mathématique de l'ordre
lexicographique, qui compare les mots lettre à lettre et tienne compte
de la longueur des mots.
Comptage d'occurrences.
Écrivez une fonction Count telle que {Count L1
L2} renvoie une liste avec le nombre de fois que chaque élément
de L2 apparaît dans L1.
La valeur retournée est une liste de paires E#N, où
E est un élément de L2 et N est
le nombre de fois que E apparaît dans L1. On
suppose qu'aucun élément n'apparaît deux fois dans L2.
Par exemple,
{Browse {Count [a b a d b c d e] [b c d]}} % affiche [b#2 c#1 d#2]
{Browse {Count [a b a d b c d e] [a g d]}} % affiche [a#2 g#0 d#2]
{Browse {Count [a b a d b c d e] nil}} % affiche nil