Séance 3
Programmation récursive avec des listes

Cette séance poursuit l'utilisation de la récursivité comme technique de programmation. Nous allons l'utiliser sur des listes. N'oubliez pas de spécifier les fonctions que vous écrivez, et d'utiliser des invariants pour garantir leur correction.

Enoncés des exercices

1. Quelques fonctions générales sur les listes. Voici une liste de fonctions à implémenter, avec quelques exemples de leur utilisation. Choisissez-en quelques-unes et programmez-les en raisonnant de manière inductive sur la structure des listes.

   • {Length Xs} renvoie la longueur de la liste Xs. La liste vide a une longueur nulle.

        {Browse {Length [r a p h]}}     % affiche 4
        {Browse {Length [[r a p] h]}}   % affiche 2
        {Browse {Length [[r a p h]]}}   % affiche 1
     

   • {Member X Ys} renvoie true si X est un élément de la liste Ys, false sinon.

        {Browse {Member p [r a p h]}}     % affiche true
        {Browse {Member c [r a p h]}}     % affiche false
        {Browse {Member p [r [a p] h]}}   % affiche false
     

   • {Append Xs Ys} renvoie la concaténation des listes Xs et Ys.

        {Browse {Append [r a] [p h]}}     % affiche [r a p h]
        {Browse {Append [r [a]] [p h]}}   % affiche [r [a] p h]
        {Browse {Append [r a] [[p h]]}}   % affiche [r a [p h]]
     

   • {Nth Xs N} renvoie le Nème élément de la liste Xs.

        {Browse {Nth [r a p h] 3}}     % affiche p
        {Browse {Nth [r [a p] h] 3}}   % affiche h
        {Browse {Nth [[r a p h]] 3}}   % quel est le resultat?
     

   • {Take Xs N} renvoie une liste contenant les N premiers éléments de la liste Xs.

        {Browse {Take [r a p h] 2}}     % affiche [r a]
        {Browse {Take [r a p h] 7}}     % affiche [r a p h]
        {Browse {Take [r [a p] h] 2}}   % quel est le resultat?
     

   • {Drop Xs N} renvoie la liste Xs sans ses N premiers éléments.

        {Browse {Drop [r a p h] 2}}     % affiche [p h]
        {Browse {Drop [r a p h] 7}}     % affiche nil
        {Browse {Drop [r [a p] h] 2}}   % quel est le resultat?
     

   • {TakeDrop Xs N Ys Zs} est une procédure qui généralise les fonctions Take et Drop. Après appel, Ys contient les N premiers éléments de Xs, le reste de Xs étant lié à Zs.

        local Ys Zs in
           {TakeDrop [r a p h] 2 Ys Zs}
           {Browse Ys}                    % affiche [r a]
           {Browse Zs}                    % affiche [p h]
        end
     

2. Multiplions. Écrivez une fonction MultList telle que {MultList L} renvoie le résultat de la multiplication des éléments de la liste L. Par exemple,

      {Browse {MultList [1 2 3 4]}}   % affiche 24
   

3. Nombres factoriels. Écrivez une fonction Fact telle que {Fact N} renvoie la liste des N premiers nombres factoriels dans l'ordre croissant. Par exemple,

      {Browse {Fact 4}}   % affiche [1 2 6 24]
   

4. Mettons les listes à plat. Écrivez une fonction Flatten prenant une liste L en paramètre. Les éléments de L peuvent eux-même être des listes, dont les éléments peuvent aussi être des listes, et ainsi de suite. L'appel {Flatten L} renvoie la liste ``aplatie'', c'est-à-dire les éléments de L et des listes contenues dans L qui ne sont pas des listes. Exemple:

      {Browse {Flatten [a [b [c d]] e [[[f]]]]}}   % affiche [a b c d e f]
   

5. Occurrences d'une sous-liste. Écrivez une fonction FindString telle que {FindString S T} renvoie la liste des occurrences de la succession de caractères S dans le texte T. Chaque occurrence est identifiée par la position de son premier caractère dans T. Par exemple,

      {Browse {FindString [a b a b] [a b a b a b]}}   % affiche [1 3]
      {Browse {FindString [a] [a b a b a b]}}         % affiche [1 3 5]
      {Browse {FindString [c] [a b a b a b]}}         % affiche nil
   

   Conseil: commencez par écrire une fonction Prefix telle que {Prefix L1 L2} renvoie true si L1 est un préfixe de L2, false sinon. Par exemple,

      {Browse {Prefix [1 2 1] [1 2 3 4]}}   % affiche false
      {Browse {Prefix [1 2 3] [1 2 3 4]}}   % affiche true
   

6. Représentation binaire d'entiers avec des listes. Écrivez une fonction Add telle que {Add B1 B2} renvoie le résultat de l'addition des nombres binaires B1 et B2. Un nombre binaire est représenté par une liste de chiffres binaires (0 ou 1). Le chiffre le plus significatif est le premier élément de la liste. Par exemple,

      {Browse {Add [1 1 0 1 1 0] [0 1 0 1 1 1]}}   % affiche [1 0 0 1 1 0 1]
   

   Quelques remarques:

   • Vous pouvez supposer que les deux listes passées en argument ont la même taille.
   • Vous devriez commencer par écrire un additionneur de trois chiffres {AddDigits D1 D2 CI}, qui prend trois chiffres binaires D1, D2 et CI, et renvoie une liste de deux chiffres binaires représentant leur somme. Le bit CI et le premier chiffre du résultat est un chiffre de report. Exemples:

        {Browse {AddDigits 1 0 0}}   % affiche [0 1]
        {Browse {AddDigits 1 1 0}}   % affiche [1 0]
        {Browse {AddDigits 1 0 1}}   % affiche [1 0]
        {Browse {AddDigits 1 1 1}}   % affiche [1 1]
     

7. Comptage d'occurrences. Écrivez une fonction Count telle que {Count L1 L2} renvoie une liste avec le nombre de fois que chaque élément de L2 apparaît L1. La valeur retournée est une liste de paires E#N, où E est un élément de L2 et N est le nombre de fois que E apparaît dans L1. On suppose qu'aucun élément n'apparaît deux fois dans L2. Par exemple,

      {Browse {Count [a b a d b c d e] [b c d]}}   % affiche [b#2 c#1 d#2]
      {Browse {Count [a b a d b c d e] [a g d]}}   % affiche [a#2 g#0 d#2]
      {Browse {Count [a b a d b c d e] nil}}       % affiche nil
   

8. Enlevons les intrus. Écrivez une fonction FilterList telle que {FilterList L1 L2} renvoie la liste résultant de L1 après avoir supprimé tous les éléments qui apparaissent dans L2. Par exemple,

   	
      {Browse {FilterList [1 2 1 4 2 3 4 5] [2 3 4]}}       % affiche [1 1 5]
      {Browse {FilterList [1 2 1 4 2 3 4 5] [20 2 3 4]}}    % affiche [1 1 5]
      {Browse {FilterList [1 2 1 4 2 3 4 5] [20 30 40]}}    % affiche [1 2 1 4 2 3 4 5]
      {Browse {FilterList [1 2 1 4 2 3 4 5] [1 2 3 4 5]}}   % affiche nil
   

9. Qui fait quoi? Nous voulons écrire un programme pour assigner automatiquement des problèmes à nos étudiants. Au départ, nous disposons d'une liste de problèmes [P1 ... PN] et une liste d'étudiants, où chaque étudiant est représenté par une liste de la forme [Email Nom]. Il y a plus d'étudiants que de problèmes, et nous voulons assigner chaque problème au même nombre d'étudiants. Vous pouvez supposer que le nombre d'étudiants est un multiple du nombre de problèmes.

   Écrivez une fonction AssignProblems telle que {AssignProblems Problems Students} renvoie une liste de listes de la forme [Email Problem] représentant l'assignation des problèmes aux étudiants. Par exemple,

      declare
      Pbs = [p1 p2]
   
      Stds = [['Roland Dyens' 'rdyens@foo.boo']
              ['Yngwie Malmsteen' 'ymalmste@foo.boo']
              ['Steve Morse' 'smorse@foo.boo']
              ['Muza Rubackyte' 'mrubacky@foo.boo']
              ['Tarja Turunen' 'tturunen@foo.boo']
              ['Frank Zappa' 'fzappa@foo.boo']]
   
      {Browse {AssignProblems Pbs Stds}}
      % affiche la liste
      % [['rdyens@foo.boo' p1]
      %  ['ymalmste@foo.boo' p2]
      %  ['smorse@foo.boo' p1]
      %  ['mrubacky@foo.boo' p2']
      %  ['tturunen@foo.boo' p1]
      %  ['fzappa@foo.boo' p2]]
   

10. Je trie, tu tries, il trie... Cet exercice consiste à implémenter des algorithmes dans le modèle déclaratif. Les algorithmes ci-dessous sont tous des algorithmes de tri. Vous devez donc implémenter autant de fonctions qui trient une liste d'entiers. Chacun des algorithmes est illustré avec la liste [5 1 7 2 6 4 3].

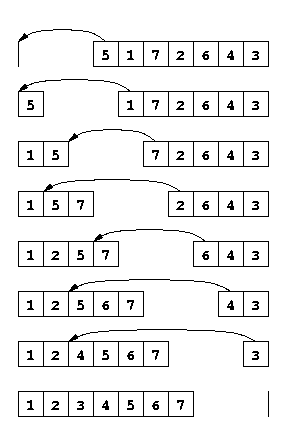
    • Tri par insertion. Il consiste à prendre les éléments de la liste un à un, et de les insérer au bon endroit dans une liste triée. A la fin, la seconde liste contient tous les éléments dans l'ordre. Conseil : Définissez une fonction qui calcule le résultat de l'insertion d'une valeur x dans une liste triée ys. Voir la figure gauche ci-dessous.

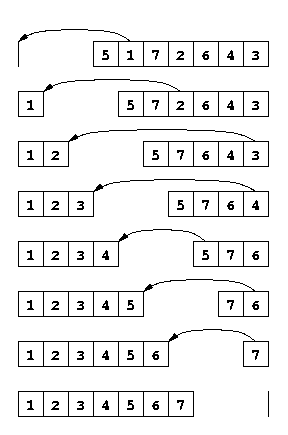
    • Tri par sélection. Il consiste à retirer de la liste l'élément le plus petit, le mettre dans le résultat, et de recommencer avec la liste restante. Les éléments sont donc retirés de la liste initiale exactement dans l'ordre du résultat final. Conseil : Définissez une fonction qui renvoie l'élément minimum d'une liste, ainsi qu'une fonction qui calcule le résultat de la suppression d'une valeur x d'une liste ys. Voir la figure droite ci-dessous.

      Exemple de tri par insertion

      Exemple de tri par sélection

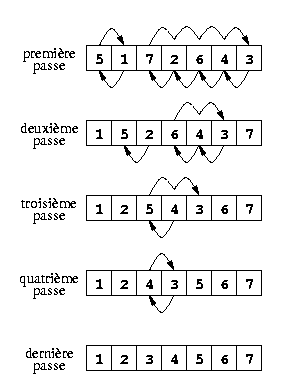
    • Tri à bulles. Il consiste à parcourir la liste en échangeant les paires d'éléments consécutifs qui ne sont pas dans l'ordre. On effectue autant de parcours que des échanges sont nécessaires. Autrement dit, on arrête dès qu'un parcours n'a fait aucun échange. Voir la figure gauche ci-dessous.

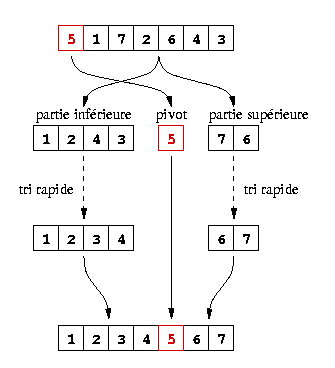
    • Tri rapide (quicksort). Cette méthode consiste à choisir une valeur pivot, et séparer les éléments de la liste en deux parties : ceux inférieurs au pivot, et ceux supérieurs au pivot. Les deux parties sont alors triées, puis concaténées (la partie inférieure avant la partie supérieure). Pour le pivot, on peut prendre le premier élément de la liste à trier. Voir la figure droite ci-dessous.

      Exemple de tri à bulles

      Exemple de tri rapide

Exercice individuel (échéance: le 28 octobre 2004)

Remplissez le formulaire avec votre réponse, ensuite sélectionnez votre tuteur dans la liste. Une fenêtre apparaîtra avec le contenu d'un e-mail que vous devrez envoyer.