Séance 5
Etat, types abstraits et objets

Dans cette séance, nous allons utiliser les cellules Oz pour implémenter des algorithmes. Nous verrons également comment les encapsuler, et programmer des objets avec de simples procédures.

Enoncés des exercices

Introduction aux cellules. Le code ci-dessous crée deux cellules et effectue des opérations pour modifier leur contenu. Indiquez quel est le contenu des cellules après chaque instruction.
```
   declare
   C1={NewCell 0}
   C2={NewCell 42}

   C1:=@C1+1
   C2:=@C1+1
   C1:=@C2+1
   C2:=@C1+1
```
Faites de même pour les deux instructions suivantes. La deuxième instruction est-elle correcte? Si oui, quel est son résultat? Sinon, expliquez pourquoi.
```
   C1:=@C2
   C2:=C1
```
Passez-moi le 22 à Asnières. Nous voulons comparer l'efficacité de deux implémentations possibles de la fonction Fibonacci.
```
   % Implementation 1
   fun {Fibonacci N}
      if N=<1 then 1 else {Fibonacci N-1}+{Fibonacci N-2} end
   end

   % Implementation 2
   fun {Fibonacci N}
      fun {Fibo I A B}
         if I>=N then B else {Fibo I+1 B A+B} end
      end
   in
      {Fibo 1 1 1}
   end
```
Utilisez une cellule pour compter le nombre d'appels récursifs effectués dans chaque cas. La cellule ne doit avoir aucun effet sur le résultat des appels à Fibonacci. Expliquez comment écrire des programmes de test pour comparer les fonctions.
Un objet pour compter. Nous allons définir un objet avec trois méthodes. L'objet implémente un compteur, et utilise une cellule pour stocker sa valeur. La cellule doit être cachée par portée lexicale, et n'est accessible que par l'intermédiaire des méthodes. Les méthodes sont implémentées par des procédures et des fonctions. Voici à quoi ressemble l'implémentation:
```
   local
      Count={NewCell 0}
   in
      fun {GetCount} ... end

      proc {IncCount} ... end

      proc {ResetCount} ... end
   end
```
La méthode GetCount renvoie la valeur courante du compteur, IncCount incrémente le compteur, et ResetCount remet le compteur à zéro. Complétez le code des trois méthodes.

Auriez-vous pu utiliser cet objet pour l'exercice précédent? Cette implémentation alternative a-t-elle des avantages par rapport à votre première solution? Lesquels?
Accumulateurs et état. Pour implémenter des fonctions efficaces dans le paradigme déclaratif, nous avons utilisé des accumulateurs dans les paramètres des fonctions. Un accumulateur est une forme d'état implicite. Un exemple typique est la fonction Reverse, qui renvoie la liste passée en argument avec ses éléments dans l'ordre inverse.
```
   fun {Reverse Xs}
      fun {ReverseAux Xs Ys}
         case Xs of nil then Ys
         [] X|Xr then {ReverseAux Xr X|Ys}
         end
      end
   in
      {ReverseAux Xs nil}
   end
```
Réécrivez cette fonction pour rendre explicite l'état passé dans l'argument Ys de ReverseAux. En d'autres mots, construisez une implémentation de la fonction qui utilise une cellule. Vous pouvez utiliser une boucle for:
```
   for X in Xs do instruction end
```
qui est équivalente à
```
   {ForAll Xs proc {$ X} instruction end}
```
L'abstraction de contrôle ForAll appelle une procédure P avec tous les éléments de la liste Xs. Elle est définie par
```
   proc {ForAll Xs P}
      case Xs of nil then skip
      [] X|Xr then {P X} {ForAll Xr P}
      end
   end
```
- A votre avis, votre fonction est-elle efficace, comparée à la définition avec accumulateur ci-dessus?
- L'état explicite que vous avez introduit est-il visible ou encapsulé? S'il est encapsulé, à quel endroit? Combien de fois créez-vous une cellule?
- Pouvez-vous également créer un état explicite pour l'argument Xs? Si c'est le cas, implémentez-le. Sinon, expliquez pourquoi.
Une calculatrice. Dans cet exercice, nous allons implémenter une calculatrice utilisant la notation postfixe (ou notation polonaise inversée). Dans cette notation, l'opérateur est écrit après ses deux opérandes. Par exemple, l'expression (13+45)*(89-17) se note "13 45 + 89 17 - *". L'avantage de cette notation est qu'elle ne nécessite pas l'utilisation de parenthèses.

L'évaluation d'une expression postfixe est très simple. On utilise une pile pour stocker les résultats intermédiaires. Il suffit de parcourir l'expression de gauche à droite, et de traiter les éléments (valeurs et opérateurs) un à un. Lorsqu'on lit une valeur, on la met sur la pile. Lorsqu'on lit un opérateur, on retire les deux valeurs au sommet de la pile, on leur applique l'opérateur, puis on met le résultat sur la pile. A la fin, la pile doit contenir une seule valeur: le résultat du calcul. Ci-dessous, de gauche à droite, les étapes du calcul de l'expression postfixe "13 45 + 89 17 - *". La ligne supérieure contient le reste de l'expression, la ligne inférieure la pile des valeurs intermédiaires.

13 45 + 89 17 - * 45 + 89 17 - * + 89 17 - * 89 17 - * 17 - * - * *

13 45 13 58 89 58 17 89 58 72 58 4176

Ecrivez une abstraction de données pile. Cette abstraction est définie par quatre opérations: NewStack, IsEmpty, Push et Pop. Push est une procédure, les autres sont des fonctions.
- {NewStack} renvoie une nouvelle pile.
- {IsEmpty S} renvoie true si la pile S passée en argument est vide, false sinon.
- {Push S X} empile l'élément X sur la pile S.
- {Pop S} enlève le sommet de la pile S et le renvoie.
Une pile est représentée par une cellule contenant une liste. La liste contient les éléments de la pile, du sommet à la base. Le premier élément de la liste est donc le sommet de la pile.

Ensuite, écrivez une fonction Eval qui prend en paramètre une expression postfixe et renvoie son évaluation. L'expression est représentée par une liste dont chaque élément est soit un entier, soit une des constantes '+', '-', '*' et '/', cette dernière devant être interprétée comme la division entière. L'expression de l'exemple ci-dessus sera représentée par la liste [13 45 '+' 89 17 '-' '*']. La fonction Eval parcourt cette liste et met à jour le contenu d'une pile, en suivant l'algorithme présenté informellement ci-dessus.
```
   {Browse {Eval [13 45 '+' 89 17 '-' '*']}}   % affiche 4176 = (13+45)*(89-17)
   {Browse {Eval [13 45 '+' 89 '*' 17 '-']}}   % affiche 5145 = ((13+45)*89)-17
   {Browse {Eval [13 45 89 17 '-' '+' '*']}}   % affiche 1521 = 13*(45+(89-17))
```

Encapsulation de l'état de la pile. Nous allons maintenant implémenter une variante de l'abstraction pile présentée dans l'exercice précédent. Cette variante rend l'état de la pile invisible à l'utilisateur. Il s'agit donc de ``cacher'' la cellule contenant la liste par portée lexicale. La fonction NewStack ne peut donc pas renvoyer directement la cellule. Elle va plutôt renvoyer une liste de fonctions et procédures:

   {NewStack} -> [IsEmpty Push Pop]

Les fonctions IsEmpty, Pop et la procédure Push sont spécifiques à la pile qui vient d'être créée. Voici un exemple d'utilisation, avec deux piles.

   declare
   [IsEmpty1 Push1 Pop1]={NewStack}   % pile 1
   [IsEmpty2 Push2 Pop2]={NewStack}   % pile 2

   {Browse {IsEmpty1}}                % affiche true; la pile 1 est vide
   {Push1 13}                         % empile 13 sur la pile 1
   {Browse {IsEmpty1}}                % affiche false; la pile 1 n'est pas vide
   {Browse {IsEmpty2}}                % affiche true; la pile 2 est toujours vide
   {Push1 45}                         % empile 45 sur la pile 1
   {Push2 {Pop1}}                     % enlève 45 de la pile 1 et l'empile sur la pile 2
   {Browse {IsEmpty2}}                % affiche false; la pile 2 n'est pas vide
   {Browse {Pop1}}                    % enlève 13 de la pile 1 et l'affiche

Voici un squelette d'implémentation pour NewStack. Complétez-le.

   fun {NewStack}
      ...
      fun {IsEmpty} ... end
      proc {Push X} ... end
      fun {Pop} ... end
   in
      [IsEmpty Push Pop]
   end

Adaptez la fonction Eval que vous avez écrite dans l'exercice précédent afin qu'elle utilise cette implémentation de l'abstraction de données pile.

Des blocs empilés dans une file... Considérez des blocs numérotés, et empilés les uns sur les autres pour former des ``tours''. Un exemple est présenté ci-dessous. Ensuite, on retire les blocs un à un, une tour après l'autre, en commençant par le bloc au sommet de chaque tour. On retire donc d'abord le sommet de chacune des tours, puis on répète l'opération avec les tours restantes. Dans l'exemple, on retire d'abord les blocs 1, 4, 6, 10, puis ceux de l'étage en-dessous, c'est-à-dire 2, 5, 7, puis 3, 8 et enfin le bloc 9.

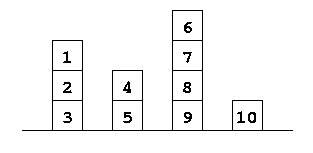
Le but de l'exercice est d'écrire une fonction RetraitBlocs qui renvoie les blocs retirés dans l'ordre indiqué. Chaque tour est représentée par une liste, les éléments apparaissant du sommet à la base. Les tours de l'exemple peuvent donc être représentées par les listes [1 2 3], [4 5], [6 7 8 9] et [10]. La fonction prend la liste des tours en paramètre, et renvoie la liste des blocs dans l'ordre de retrait.
```
   {Browse {RetraitBlocs [[1 2 3] [4 5] [6 7 8 9] [10]]}}   % affiche [1 4 6 10 2 5 7 3 8 9]
```
L'implémentation est basée sur l'abstraction de données file. Cette abstraction est similaire à une pile. La différence est que les éléments sont extraits dans l'ordre où ils ont été insérés, tandis que dans une pile, les éléments sont extraits dans l'ordre inverse où ils ont été empilés. Dans une file, les premiers rentrés sont les premiers sortis. L'abstraction est définie par les quatre opérations NewQueue, IsEmpty, Enqueue et Dequeue. Voici une implémentation simple d'une file, sous la forme ``encapsulée''. Les commentaires spécifient les opérations.
```
   %% renvoie une nouvelle file
   fun {NewQueue}
      Q={NewCell nil}

      %% renvoie true ssi la file est vide
      fun {IsEmpty} @Q==nil end

      %% insère X dans la file
      proc {Enqueue X}
         Q:={Append @Q [X]}
      end

      %% enlève un élément de la file et le renvoie
      fun {Dequeue}
         case @Q of X|T then Q:=T  X end
      end
   in
      [IsEmpty Enqueue Dequeue]
   end
```
La fonction RetraitBlocs doit procéder de la façon suivante. On commence par mettre toutes les tours dans la file. Ensuite, on extrait une tour de la file. Si la tour contient au moins un bloc, on retire ce bloc et on insère la tour sans ce bloc dans la file. Si la tour est vide, on ne fait rien. On répète l'opération jusqu'à ce que la file soit vide.

Implémentez la fonction RetraitBlocs en utilisant l'abstraction file proposée ci-dessous.
Une file avec deux piles. L'implémentation de la file dans l'exercice précédent n'est pas très efficace. L'opération Enqueue doit parcourir tous les éléments présents pour ajouter un élément. Si la file contient beaucoup d'éléments, cette opération peut s'avérer très lente.

Dans cet exercice, vous allez implémenter une file avec deux piles. Le schéma ci-dessous illustre le fonctionnement de l'implémentation. Le sommet de la première pile correspond à l'avant de la file, tandis que le sommet de la seconde pile correspond à l'arrière de la file. Lorsque la première pile est vide, la seconde peut être ``retournée'' sur la première. Ce retournement est utilisé pour retirer l'élément en tête de file lorsque la pile correspondant à l'avant est vide. On peut montrer que le temps moyen des opérations Enqueue et Dequeue est constant, et ne dépend donc pas de la taille de la file.

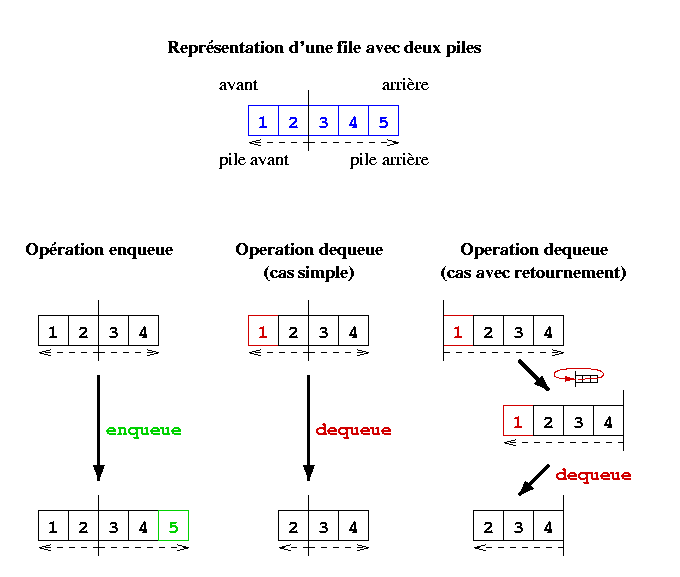
Ecrivez l'implémentation de l'abstraction file en utilisant cette technique, sous forme encapsulée ou non (au choix). Utilisez une des implémentations des exercices précédents pour les piles.

Si vous utilisez la forme encapsulée, que faut-il modifier dans la fonction RetraitBlocs de l'exercice précédent pour qu'elle utilise cette nouvelle implémentation?

Exercice individuel

Remplissez le formulaire avec votre réponse, ensuite sélectionnez votre tuteur dans la liste. Une fenêtre apparaîtra avec le contenu d'un e-mail que vous devrez envoyer.

Parenthésage. Nous allons vérifier qu'une expression est correctement parenthésée. Pour cela, on retire de l'expression tous les termes sauf les parenthèses, puis on vérifie que chaque parenthèse ouvrante correspond à une et une seule parenthèse fermante du même type. Ainsi, les parenthèses '(', '[' et '{' doivent correspondre respectivement à ')', ']' et '}'.

Ecrivez une fonction BienParenthese qui prend une liste de caractères représentant des parenthèses, et renvoie true si l'expression est bien parenthésée, false sinon. La technique suggérée utilise une pile. Les parenthèses ouvrantes sont mises sur la pile. Pour chaque parenthèse fermante, on retire un élément de la pile et on vérifie que c'est la parenthèse ouvrante correspondante.
```
   {Browse {BienParenthese ['{' '(' ')' '[' '(' ')' ']' '}']}}   % affiche true
   {Browse {BienParenthese ['{' '(' ')']}}   % affiche false: pas de correspondante pour '{' 
   {Browse {BienParenthese ['{' '(' ')' ']']}}   % affiche false: '{' ne correspond pas a ']'
```

Sélectionnez maintenant le nom de votre tuteur dans la liste :

Raphaël Collet - 5 novembre 2004

`13 45 + 89 17 - *`	`45 + 89 17 - *`	`+ 89 17 - *`	`89 17 - *`	`17 - *`	`- *`	`*`
	`13`	`45 13`	`58`	`89 58`	`17 89 58`	`72 58`	`4176`

Séance 5 Etat, types abstraits et objets

Enoncés des exercices

Exercice individuel

Séance 5
Etat, types abstraits et objets