| LINF1251 - Page des travaux pratiques |
Ce travail porte sur la mise en oeuvre de techniques de la programmation déclarative pour résoudre un problème plus conséquent que ceux proposés dans les séances d'exercices.
Les modalités sont les suivantes :
Le travail est réalisé en groupe de deux étudiants (ou seul si ce n'est pas possible).
Le travail est obligatoire et compte pour 5 points dans votre note finale.
La date limite pour la remise est le mercredi 11 mai. L'évaluation se fera principalement par une interview avec l'assistant, pendant l'un des créneaux horaires à définir (vraissemblablement entre le 11 et le 13 mai).
Par ailleurs, les fichiers seront envoyés par courrier électronique
à jfallon@info.ucl.ac.be, si
possible sous forme comprimée (format ZIP, par
exemple).
En cas de problème, envoyez un mail à jfallon@info.ucl.ac.be.
Concernant les programmes produits :
Les programmes doivent être courts et simples. Préférez un programme clair et raisonnablement efficace à un programme rapide mais difficile à comprendre.
Les programmes doivent être documentés.
Les critères d'évaluation du travail sont la correction , la simplicité et la lisibilité des programmes.
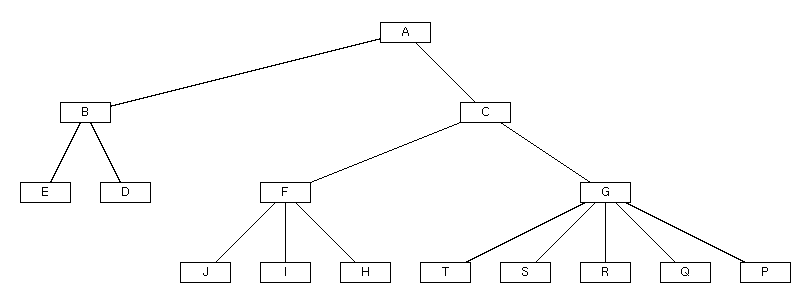
Le travail consiste à implémenter un système de représentation d'arbres dans le modèle du calcul déclaratif vu au cours. La partie principale du travail consistera à implémenter l'algorithme assignant des positions aux noeuds de l'arbre. Le système prendra en entrée un fichier contenant des relations père-fils, de la forme : "père engendra fils1 et fils2 et fils3". Comme résultat, le système devra afficher à l'écran l'arbre dessiné. Certaines parties ont déjà été implémentées pour vous. Afin de les récupérer efficacement, il vous est proposé de "découper" le système de la façon suivante (les différentes étapes sont illustrées sur la figure qui suit les explications) :
filiation(pere:Label fils:[Label1 Label2]), ayant comme champ le label du père (un atom), et une liste contenant les labels des fils (des atom également). Le parseur vous est fourni.
tree(label:Label fils:[tree(...) tree(...) ...]).
posTree(label:Label xPos:XPos yPos:YPos fils:[...]).

A engendra B et C
B engendra D et E
C engendra G et F
F engendra H et I et J
G engendra P et Q et R et S et T
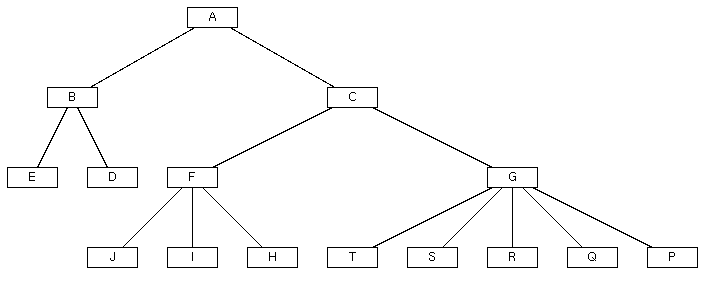
D est au-dessus de J, alors qu'il n'y a pas de lien entre eux.
 |
 |
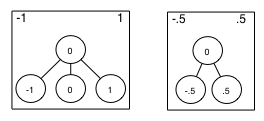
filiation faite à la main. make dans une fenêtre de terminal, en étant dans le répertoire de vos sources. Cette commande permet de compiler les ressources en une fois.
% charger le module (une fois)
declare
[BibleParser]={Module.link["BibleParser.ozf"]}
ParseGenese=BibleParser.parseGenese
% importer la liste de structure
L={ParseGenese "CheminFichier.txt"}
% charger le module (une fois)
declare
[Displayer]={Module.link["http://www.info.ucl.ac.be/people/PVR/ds/LINF1251/projet/ressources/Displayer.ozf"]}
Display=Displayer.display
% afficher un arbre Arbre avec un FacteurDeZoom specifié (par exemple 80.0)
{Display Arbre FacteurDeZoom}