Exercices résolus

Cette page contient une série d'exercices résolus. Ces exercices sont des variantes de certains exercices proposés en séance.

Enoncés des exercices

Premier diviseur. Cet exercice est une variante de l'exercice Test de primalité de la séance 2. Écrivez une fonction PremierDiviseur avec un paramètre entier N qui renvoie le plus petit diviseur de N. On suppose que N ≥ 2, de telle sorte que le diviseur est compris entre 2 et N.

Ensuite, utilisez la propriété mentionnée dans l'exercice original pour améliorer l'efficacité de votre fonction. La propriété implique que si N n'est pas premier, alors son plus petit diviseur est inférieur ou égal à la racine carrée de N. Dans le cas où N est premier, le plus petit diviseur est N lui-même.

Solution. Cette solution consiste à écrire une fonction auxiliaire qui va tester les entiers entre 2 et N, et renvoyer le premier qui divise N. L'invariant de cette fonction auxiliaire doit permettre de prouver que l'entier renvoyé est bien le plus petit diviseur. Il est écrit en commentaire dans le code.
```
   %% renvoie le plus petit diviseur de N (N>=2)
   fun {PremierDiviseur N}
      %% invariant: I=<N et aucun K tel que 2=<K<I ne divise N
      fun {PremierAux I}
         if N mod I==0 then I else {PremierAux I+1} end
      end
   in
      {PremierAux 2}
   end
```
Voici maintenant l'optimisation demandée. On modifie la définition de PremierAux en testant d'abord si I² est inférieur ou égal à N. Si ce n'est pas le cas, on renvoie immédiatement N.
```
   %% renvoie le plus petit diviseur de N (N>=2)
   fun {PremierDiviseur N}
      %% invariant: aucun K tel que 2=<K<I ne divise N
      fun {PremierAux I}
         if I*I>N then N else
            if N mod I==0 then I else {PremierAux I+1} end
         end
      end
   in
      {PremierAux 2}
   end
```

Numérotation des points du plan. Cet exercice est une variante de l'exercice Numérotation des points du plan de la séance 2. Comme dans cet exercice, nous allons affecter un entier naturel a chaque couple d'entiers naturels (x, y). La figure suivante illustre la technique, qui consiste à numéroter les points situés dans des carrés de taille croissante. Les numéros des points sont en bleu.

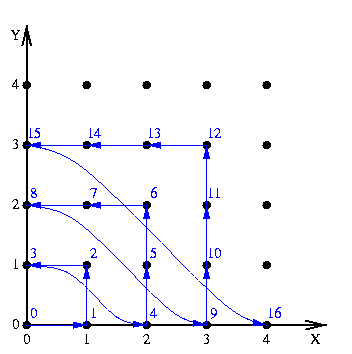
Numérotation des points du plan

Ecrivez une fonction Numero, prenant en paramètre deux naturels x et y, et renvoyant leur numéro suivant la technique illustrée ci-dessus. Nous proposons deux techniques.

Exprimez le numéro d'un point en fonction du numéro de son prédécesseur. Le prédécesseur est défini en suivant les flèches bleues en arrière. Par exemple, les prédécesseurs successifs de (3, 2) sont (3, 1), (3, 0), (0, 2), (1, 2), ... Implémentez une version itérative de Numero.
Améliorez l'efficacité de votre fonction sur base des trois observations suivantes. Si x ≤ y, le point (x, y) se trouve sur la même droite horizontale que le point (y, y). Si y ≤ x, le point (x, y) se trouve sur la même droite verticale que le point (x, 0). Enfin, le numéro d'un point sur l'axe des X, de la forme (x, 0), correspond au nombre de points dans le carré de côté (0, 0) (x-1, 0). Et ce côté comporte x points...
Etant donné un numéro n, pouvez-vous retrouver les coordonnées (x, y) du point correspondant? Aide: Trouvez d'abord la racine carrée entière de n, disons r. On voit facilement que le point (x, y) est sur le côté droit ou le côté supérieur du carré de base (0, 0) (r, 0). Ensuite, déterminez sur quel côté du carré se trouve le point numéro n. Vos fonctions sont-elles itératives? Quel est leur invariant?

Solution. Regardons d'abord comment suivre les flèches bleues en arrière. Plusieurs cas se présentent, suivant qu'un point se trouve dans le coin inférieur droit, sur le côté droit ou sur le côté supérieur d'un carré. Voici les équations établissant les relations entre les numéros de ces points.

numero(0, 0) = 0
numero(x, 0) = numero(0, x-1) + 1		si 0 < x (coin inférieur droit)
numero(x, y) = numero(x, y-1) + 1		si 0 < y ≤ x (côté droit)
numero(x, y) = numero(x+1, y) + 1		si x < y (côté supérieur)

On dérive alors facilement une fonction Numero basée sur ces équations. Nous donnons immédiatement une version itérative, utilisant un accumulateur Acc pour calculer le numéro.

   %% renvoie le numero du point (X,Y)
   fun {Numero X Y}
      %% invariant: numero(X,Y)=numero(A,B)+Acc
      fun {NumeroAux A B Acc}
         if B==0 then
            if A==0
	    then Acc                       % (0,0)
            else {NumeroAux 0 A-1 Acc+1}   % coin inferieur droit
            end
         else
            if B=<A
	    then {NumeroAux A B-1 Acc+1}   % cote droit
            else {NumeroAux A+1 B Acc+1}   % cote superieur
            end
         end
      end
   in
      {NumeroAux X Y 0}
   end

Nous allons maintenant utiliser des propriétés de la numérotation pour calculer directement certains numéros. Les équations suivantes sont faciles à comprendre et à vérifier (on peut s'inspirer du schéma ci-dessus).

numero(x, 0) = xx*		(coin inférieur droit)
numero(x, y) = numero(x, 0) + y		si 0 ≤ y ≤ x (côté droit)
numero(x, y) = numero(y, y) + (y-x)		si x ≤ y (côté supérieur)

Voici une version de Numero qui utilise ces relations. On voit facilement sur les équations que le nombre d'appels récursifs est au maximum 3. Il n'est donc pas nécessaire de rendre cette version itérative. A titre d'exercice, on peut même combiner tous les cas et éviter toute récursivité...

   %% renvoie le numero du point (X,Y)
   fun {Numero X Y}
      if Y==0
      then X*X                       % coin inferieur droit
      else if Y=<X
           then {Numero X 0}+Y       % cote droit
           else {Numero Y Y}+(Y-X)   % cote superieur
           end
      end
   end

Enfin, déterminons les coordonnées du point de numéro n. Calculons d'abord la racine carrée entière de n. Voici une fonction qui cherche cette valeur itérativement, à partir de zéro.

   %% renvoie la racine carree entiere de N
   fun {RacineCarree N}
      %% invariant: I*I=<N
      fun {Iter I}
         if N<(I+1)*(I+1)
         then I   % car I=<racine(N)<I+1
         else {Iter I+1}
         end
      end
   in
      {Iter 0}
   end

Soit r la racine carrée entière de n. Les points (r, 0), (r, r) et (0, r) portent respectivement les numéros r², r² + r et r² + 2 r. En comparant n à ces valeurs, on détermine sur quel côté se trouve le point recherché. Ses coordonnées se déduisent facilement. Voici une procédure qui lie ses arguments X et Y aux coordonnées respectives du point numéro N.

   %% renvoie les coordonnees (X,Y) du point numerote N
   proc {Coordonnees N X Y}
      R={RacineCarree N}
   in
      if N=<R*R+R then   % cote droit
         X=R
         Y=N-R*R
      else   % cote superieur
         X=R*R+2*R-N
         Y=R
      end
   end

Pour utiliser cette procédure, il est nécessaire de lui fournir deux variables non affectées pour X et Y. Par exemple,

   local X Y in
      {Coordonnees 14 X Y}
      {Browse X}   % affiche 1
      {Browse Y}   % affiche 3
   end

Retrait. Cet exercice est une variante de l'exercice Qui a la plus longue? de la séance 3. Ecrivez une fonction Remove qui prend en argument une liste L et une valeur X, et qui renvoie la liste dont on a supprimé la première occurrence de X. Si X n'apparaît pas dans L, alors L est renvoyée. Par exemple,

   {Browse {Remove [1 2 3 4 5] 3}}   % affiche [1 2 4 5]
   {Browse {Remove [1 2 3 4 3] 3}}   % affiche [1 2 4 3]
   {Browse {Remove [1 2 3 4 5] 7}}   % affiche [1 2 4 3 5]

Solution. L'idée est simple: si la liste n'est pas vide, on compare son élément de tête avec X. S'ils sont égaux, on renvoie la queue de la liste. Sinon, on renvoie la tête suivie de la queue dont on a supprimé la première occurrence de X.

   %% renvoie L sans la premiere occurrence de X
   fun {Remove L X}
      if L==nil
      then nil
      else if {Head L}==X
           then {Tail L}
           else {Head L}|{Remove {Tail L} X}
           end
      end
   end

Voici une version équivalente, mais cette fois en utilisant le pattern matching.

   fun {Remove L X}
      case L
      of nil then nil
      [] H|T andthen H==X then T
      [] H|T then H|{Remove T X}
      end
   end

Suite de Fibonacci. Dans cette variante de l'exercice Nombres factoriels de la séance 3, on demande d'écrire une fonction Fibonacci telle que {Fibonacci N} renvoie la liste des N premiers nombres de Fibonacci. On suppose que N>1 et que les deux premiers nombres de la suite sont 1 et 1.
```
   {Browse {Fibonacci 10}}   % affiche [1 1 2 3 5 8 13 21 34 55]
```
Solution. Nous allons de suite concevoir une solution itérative. Pour rappel, chaque nombre de la suite est la somme des deux nombres précédents. L'idée est de partir des deux premiers nombres, puis de calculer le suivant, et ainsi de suite. Nous allons utiliser deux nombres consécutifs comme accumulateurs. Ainsi, on peut progresser dans la suite sans avoir à mémoriser autre chose qu'un compteur. On part donc de la paire (1,1), puis on passe à (1,2), puis (2,3), (3,5), etc.
```
   %% renvoie la liste des N premiers nombres de Fibonacci
   fun {Fibonacci N}
      %% invariant: A=fib(I) et B=fib(I+1)
      fun {Loop I A B}
         if I<N then A|{Loop I+1 B A+B} else [A] end
      end
   in
      {Loop 1 1 1}
   end
```

Retenons les suspects. Cet exercice est une variante de l'exercice Enlevons les intrus de la séance 5. Écrivez une fonction FilterPositiveList telle que {FilterLPositiveist L1 L2} renvoie la liste résultant de L1 après avoir supprimé tous les éléments qui n'apparaissent pas dans L2. Par exemple,

   
   {Browse {FilterPositiveList [1 2 1 4 2 3 4 5] [2 3 4]}}       % affiche [2 4 2 3 4]
   {Browse {FilterPositiveList [1 2 1 4 2 3 4 5] [20 2 3 4]}}    % affiche [2 4 2 3 4]
   {Browse {FilterPositiveList [1 2 1 4 2 3 4 5] [20 30 40]}}    % affiche nil
   {Browse {FilterPositiveList [1 2 1 4 2 3 4 5] [1 2 3 4 5]}}   % affiche [1 2 1 4 2 3 4 5]

Solution. L'appel {FilterPositiveList L1 L2} parcourt la liste L1 et renvoie dans une liste ses éléments qui sont membres de L2. La fonction est très simple et fait appel à la fonction Member dont la définition est rappelée ici.

   %% renvoie true si X est element de Ys, false sinon
   fun {Member X Ys}
      case Ys
      of nil then false
      [] Y|Yr then X==Y orelse {Member X Yr}
      end
   end

   %% renvoie les elements de L1 qui sont membres de L2
   fun {FilterPositiveList L1 L2}
      case L1
      of nil then nil
      [] X|T andthen {Member X L2} then X|{FilterPositiveList T L2}
      [] X|T then {FilterPositiveList T L2}
      end
   end

Trions encore... Cet exercice est une variante de l'exercice Je trie, tu tries, il trie... de la séance 5. Il s'agit d'implémenter un algorithme de tri dans le modèle déclaratif. L'algorithme doit être implémenté par une fonction qui trie une liste d'entiers.
- Le "strand sort". Cet algorithme se base sur la fusion de deux listes triées, qui donne une liste triée dont les éléments sont l'union des deux listes. On commence par extraire de la liste originale le plus long préfixe trié. Ensuite, on extrait de la liste restante le plus long préfixe trié et on le fusionne avec le premier. On répète l'opération jusqu'à ce que la liste restante soit vide. Conseil : Définissez une fonction Merge qui calcule la fusion de deux listes triées. L'algorithme est illustré ci-dessous avec la liste d'entiers [9 6 7 10 2 3 4 8 1 5]. Les éléments en rouge sont le plus long préfixe trié de chaque liste restante. La fusion se fait avec la liste à gauche, qui est toujours triée.
  
  Exemple de strand sort
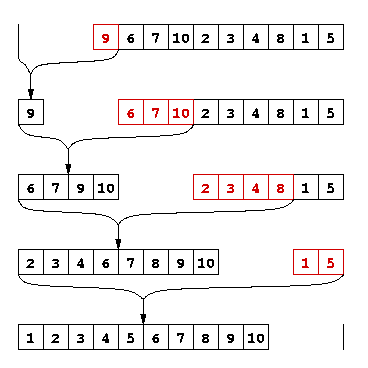
Solution. Commençons par définir la fonction Merge qui fusionne deux listes. Son principe est relativement simple. Comme les deux listes sont triées, le premier élément du résultat est le premier élément d'une des deux listes données. Par exemple, dans l'appel {Merge [3 5 7] [1 4 8]}, le premier élément du résultat est 1, c'est-à-dire le premier élément de la seconde liste.
```
   %% renvoie la fusion des listes triees Xs et Ys
   fun {Merge Xs Ys}
      case [Xs Ys]
      of [nil Ys] then Ys
      [] [Xs nil] then Xs
      [] [X|Xr Y|Yr] then % selectionne le minimum et fusionne le reste
         if X=<Y then X|{Merge Xr Ys} else Y|{Merge Xs Yr} end
      end
   end
```
Ensuite, nous devons pouvoir extraire le plus long préfixe trié d'une liste. Le principe est simple. Le premier élément de la liste fait toujours partie du résultat. On regarde les deux premiers éléments de la liste. S'ils sont en ordre, on prend le premier et on regarde les deux suivants. Sinon, on renvoie le premier élément seul.
```
   %% renvoie le plus long prefixe trie de L (L est non vide)
   fun {TakeSorted Xs}
      case Xs
      of X1|X2|Xr andthen X1=<X2 then X1|{TakeSorted X2|Xr}
      [] X|Xr then [X]
      end
   end
```
On doit ensuite calculer la liste restante. Une solution possible est d'enlever n éléments de la liste, où n est la longueur du plus long préfixe trié. On utilise les fonctions Length et Drop définies dans la séance 3. Une autre possibilité est de modifier TakeSorted pour qu'elle renvoie cette liste restante. Comme la nouvelle fonction a deux sorties, nous la définissons comme une procédure avec un paramètre d'entrée et deux paramètres de sortie. Cette procédure est baptisée TakeDropSorted.
```
   %% renvoie le plus long prefixe trie Ps de L et Rs
   %% tels que L={Append Ps Rs}
   proc {TakeDropSorted Xs Ps Rs}
      case Xs
      of X1|X2|Xr andthen X1=<X2 then Pr in
         Ps=X|Pr {TakeDropSorted X2|Xr Pr Rs}
      [] X|Xr then Ps=[X] Rs=Xr
      end
   end
```
Nous pouvons maintenant définir la fonction de tri. L'algorithme suggère naturellement d'utiliser une fonction auxiliaire avec un accumulateur. L'accumulateur Sorted est la liste triée des éléments déjà traités.
```
   %% renvoie la liste L triee
   fun {StrandSort L}
      %% invariant: il existe Zs tel que L={Append Zs Xs} et
      %%            les element de Zs sont tries dans Sorted
      fun {StrandIter Xs Sorted}
         if Xs==nil then Sorted else
            Ps Rs in
            {TakeDropSorted Xs Ps Rs}
            {StrandIter Rs {Merge Sorted Ps}}
         end
      end
   in
      {StrandIter L nil}
   end
```
Arbre de codage. Dans cette variante de l'exercice Promenade arboricole de la séance 6, nous allons utiliser un arbre binaire pour décoder une suite de bits. L'idée est la suivante: l'arbre contient dans chacune de ses feuilles un caractère. Voici un exemple d'un tel arbre, où les feuilles sont les carrés.

Un arbre de codage avec les lettres n, e, i, r et t

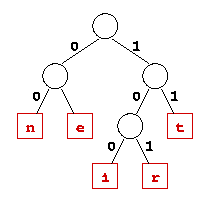
Le codage lui-même est une suite de bits. Le codage d'une lettre représente le chemin dans l'arbre de la racine vers la feuille contenant cette lettre. Lorsqu'on va vers un fils gauche, on émet un 0, lorsqu'on va vers un fils droit, on émet un 1. Dans la figure, on a indiqué le bit correspondant à chaque branche. Par exemple, la lettre i est codée comme la suite (1,0,0). Notez que les lettres ont des codes de longueurs différentes.

Choisissez une représentation de l'arbre ci-dessus avec des enregistrements. Les lettres sont représentées par les atomes e, i, n, r et t. Ensuite, écrivez une fonction Decode qui prend en arguments un arbre de codage et une liste de bits (nombres 0 et 1), et renvoie la liste des lettres correspondant à ce code. Décodez la suite
```
   [1 0 0 0 0 1 1 0 1 1 0 1 0 0 0 1 1 1]
```
Solution. Pour représenter l'arbre, nous utilisons la grammaire ci-dessous. Les feuilles de l'arbre sont représentées par un enregistrement de type leaf(X), où X est une lettre. Les autres noeuds de l'arbre ne contiennent pas d'information propre, ils ont simplement deux fils. Pour faire un lien avec le codage, les fils auront comme noms de champs 0 et 1.

<arbre> ::= leaf(<lettre>) | tree(0:<arbre> 1:<arbre>)

L'arbre de codage de l'exemple est donc donné par la valeur
```
   Arbre = tree(0:tree(0:leaf(n)
                       1:leaf(e))
                1:tree(0:tree(0:leaf(i)
                              1:leaf(r))
                       1:leaf(t)))
```
Pour la fonction Decode, le schéma est relativement simple. Il faut parcourir l'arbre en suivant la suite de bits. Lorsque l'arbre est réduit à une feuille, il faut "émettre" la lettre se trouvant dans la feuille et poursuivre le décodage à partir de l'arbre initial. Il faut donc se définir une fonction auxiliaire qui va retenir l'arbre en cours. Notez que les noms de champs permettent d'accéder par sélection au sous-arbre voulu.
```
   %% decode la suite Bits
   fun {Decode Tree Bits}
      fun {Loop T Bs}
         case T of leaf(X) then
            X|{Loop Tree Bs}
         else
            %% T est de la forme tree(0:T1 1:T2)
            case Bs
            of nil  then nil
            [] B|Br then {Loop T.B Br}
            end
         end
      end
   in
      {Loop Tree Bits}
   end
```
On fait un appel récursif par bit de la liste à décoder et par lettre décodée. Les autres opérations ont une complexité en temps constante. Si n est la longueur de Bits et m celle de la liste résultat, la complexité de Decode est O(n+m), ou plus simplement O(n). Décodons maintenant la liste demandée:
```
   {Browse {Decode Arbre [1 0 0 0 0 1 1 0 1 1 0 1 0 0 0 1 1 1]}}   % affiche [i n t e r n e t]
```

Dernier élément d'une liste. Cet exercice est une variante de l'exercice Minimum d'une liste de la séance 9. Considérez le programme ci-dessous, qui définit une fonction Last. L'appel {Last Xs} renvoie le dernier élément de la liste Xs.

   local
      fun {Last Xs}
         case Xs of X|Xr then
            if Xr==nil then X else {Last Xr} end
         end
      end
   in
      {Browse {Last [5 8 3]}}
   end

Traduisez ce programme en langage noyau, puis exécutez-le en suivant les règles de la sémantique. Pour la traduction en langage noyau, n'oubliez pas que les fonctions sont des procédures, et que le calcul des sous-expressions nécessite l'introduction de variables.

Solution. Tout d'abord, nous devons traduire l'instruction en langage noyau. La fonction devient une procédure avec un argument de sortie Z. Notez que l'instruction case requiert une clause else en langage noyau. La fonction Last ne définissant rien dans ce cas, il est nécessaire d'y placer une instruction qui provoque une erreur à l'exécution. C'est ce que fait l'instruction raise. Nous ne détaillerons pas cette instruction ici, car cela ne fait pas partie du cours. Afin d'alléger les notations dans la suite, nous avons donné un nom aux principales instructions du code (S1 à S15). Chaque instruction est délimitée par un rectangle de couleur.

Passons maintenant à l'exécution. On considère une pile sémantique avec l'instruction S1. On suppose qu'une variable browse est donnée, et que cette variable est liée à une procédure d'affichage. L'environnement de l'instruction S1 associe l'identificateur Browse à cette variable. En-dessous de la pile sémantique se trouve la mémoire du programme.

S1, {Browse→browse}

browse

L'exécution de S1 crée les variables last, l1, l2, l3, l4 et res en mémoire. Après quoi la séquence d'instructions S2 S10 S11 S12 S13 S14 S15 est placée sur la pile sémantique, avec l'environnement de S1 auquel on a ajouté les associations des identificateurs déclarés.

S2 S10 S11 S12 S13 S14 S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last, l1, l2, l3, l4, res

Pour exécuter la séquence d'instructions, on doit d'abord exécuter la première instruction. La pile sémantique est transformée en

S2,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

S10 S11 S12 S13 S14 S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last, l1, l2, l3, l4, res

L'instruction S2 crée une procédure en mémoire et lie la variable last (image de Last dans l'environnement) à cette procédure. L'environnement contextuel de la procédure est constitué de l'environnement de S2 limité aux identificateurs libres de la procédure. Dans la procédure, seul Last n'est pas déclaré. L'environnement contextuel est donc {Last→last}.

S10 S11 S12 S13 S14 S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1, l2, l3, l4, res

L'exécution de la séquence S10 S11 S12 S13 S14 S15 met l'instruction S10 en ``évidence''. Nous passons cette étape et exécutons directement S10. Cette instruction affecte la variable dénotée par L1 à une liste. La mémoire est donc mise à jour.

S11 S12 S13 S14 S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2, l3, l4, res

Les instructions S11, S12 et S13 sont également des affectations. Après leur exécution, il reste la séquence d'instructions S14 S15. La séquence est ``découpée'' et l'état de la machine est donc

S14,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res

L'instruction S14 est un appel de procédure. On remplace donc cette instruction sur la pile sémantique par le code de la procédure last. L'environnement associé est l'environnement contextuel de la procédure ({Last→last}), auquel on ajoute les associations des paramètres. Les arguments de l'appel sont les variables correspondant à L1 et Res, à savoir l1 et res. On associe la première variable à Xs et la seconde à Z.

S3,
  {Last→last, Xs→l1, Z→res}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res

L'instruction S3 est une instruction case. La valeur de Xs, c'est-à-dire l1, correspond au pattern. L'instruction sur la pile devient donc S4, avec l'environnement de S3 auquel on a ajouté les associations du pattern (X correspond à 5 et Xr correspond à l2).

S4,
  {Last→last, Xs→l1, Z→res,
  X→5, Xr→l2}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res

L'instruction S4 crée une variable cond1 en mémoire, et l'associe à Cond dans l'environnement de S5 S6.

S5 S6,
  {Last→last, Xs→l1, Z→res,
  X→5, Xr→l2, Cond→cond1}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res, cond1

L'instruction S5 compare alors Xr (l2) à nil, ce qui affecte false à Cond (cond1). Après cela, l'instruction if dans S6 se réduit à sa deuxième clause. Cela donne

S8,
  {Last→last, Xs→l1, Z→res,
  X→5, Xr→l2, Cond→cond1}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res, cond1=false

L'instruction S8 est à nouveau un appel à la procédure last avec comme arguments les variables dénotées par Xr (l2) et Z (res). L'appel est donc remplacé par le code de la procédure, et l'environnement de ce code est {Last→last, Xs→l2, Z→res}.

S3,
  {Last→last, Xs→l2, Z→res}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res, cond1=false

L'exécution de S3 avec ce code est similaire au cas précédent. On crée une variable cond2 qui est ensuite liée à false, puis on fait un appel récursif avec les variables l3 et res. On obtient

S3,
  {Last→last, Xs→l3, Z→res}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res, cond1=false, cond2=false

Le pattern de l'instruction S3 correspond avec X=3 et Xr=l4. On a donc

S4,
  {Last→last, Xs→l3, Z→res,
  X→3, Xr→l4}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res, cond1=false, cond2=false

L'instruction S4 crée la variable cond3 associée à Cond. Puis l'instruction S5 compare Xr (l4) à nil, ce qui affecte true à cond3. On a

S6,
  {Last→last, Xs→l3, Z→res,
  X→3, Xr→l4, Cond→cond3}

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res, cond1=false, cond2=false, cond3=true

L'instruction if dans S6 se réduit alors à sa première clause, c'est-à-dire S7. Cette instruction affecte X (3) à Z (res).

S15,
  {Browse→browse, Last→last, L1→l1,
  L2→l2, L3→l3, L4→l4,
  Res→res}

browse, last=⟨proc{$ Xs Z} S3 end, {Last→last}⟩, l1=5|l2, l2=8|l3, l3=3|l4, l4=nil, res=3, cond1=false, cond2=false, cond3=true

Reste alors à l'instruction S15 à afficher la valeur de Res (res), c'est-à-dire 3. Cet élément est bien le dernier de la liste [5 8 3].

On voit que l'exécution de la fonction Last crée des variables en mémoire (les variables cond), mais que ces variable disparaissent rapidement des environnements des instructions. On observe également que les appels récursifs à Last ne font pas grandir la taille de la pile sémantique plus que nécessaires. La fonction Last est donc itérative.

Une calculatrice préfixe. Cet exercice est une variante de l'exercice Une calculatrice de la séance 10. Dans cet exercice, nous allons implémenter une calculatrice utilisant la notation préfixe. Dans cette notation, l'opérateur est écrit avant ses deux opérandes. Par exemple, l'expression (13+45)*(89-17) se note "* + 13 45 - 89 17". Cette notation, comme la notation postfixe, ne nécessite pas l'utilisation de parenthèses.

L'évaluation d'une expression préfixe est un peu plus complexe qu'une expression postfixe. On utilise une pile pour stocker les résultats intermédiaires et les opérateurs non encore appliqués. Cette pile possède un invariant que nous allons utiliser: deux valeurs ne sont jamais contiguës dans la pile. Cela implique que l'élément en-dessous d'une valeur dans la pile est toujours un opérateur. Cet invariant provient du fait que chaque opérateur est appliqué dès que ses deux opérandes sont connues.

Décrivons maintenant l'algorithme. L'exemple ci-dessous illustre, de gauche à droite, les étapes du calcul de l'expression préfixe "* + 13 45 - 89 17". La ligne supérieure contient le reste de l'expression, la ligne inférieure la pile. On parcourt l'expression de gauche à droite et on traite les éléments (valeurs et opérateurs) un à un. Lorsqu'on lit un opérateur, on le met sur la pile. Lorsqu'on lit une valeur, deux cas se présentent. Si l'élément au sommet de la pile est un opérateur, on met la valeur sur la pile. La valeur est la première opérande de l'opérateur. Si l'élément au sommet de la pile est une valeur, alors on la retire de la pile, on retire ensuite l'opérateur qui se trouvait en-dessous et on applique l'opérateur. On traite alors la valeur obtenue comme si elle provenait de la liste originale. Les opérations appliquées sont marquées en rouge dans l'exemple. A la fin, la pile contient le résultat du calcul.

* + 13 45 - 89 17 + 13 45 - 89 17 13 45 - 89 17 45 - 89 17 58 - 89 17 - 89 17 89 17 17 72 4176

* + * 13 + * * 58 * - 58 * 89 - 58 * 58 * 4176

Ecrivez une abstraction de données pile. Une pile est représentée par une cellule contenant une liste, la liste contienant les éléments de la pile, du sommet à la base. Implémentez les quatre opérations standard sur les piles, à savoir NewStack, IsEmpty, Push et Pop. Push est une procédure, les autres sont des fonctions.

Ensuite, écrivez une fonction EvalPrefix qui prend en paramètre une expression préfixe et renvoie son évaluation, en suivant l'algorithme proposé ci-dessus. L'expression est représentée par une liste dont chaque élément est soit un entier, soit une des constantes '+', '-', '*' et '/', cette dernière devant être interprétée comme la division entière. L'expression de l'exemple ci-dessus sera représentée par la liste ['*' '+' 13 45 '-' 89 17].
```
   {Browse {EvalPrefix ['*' '+' 13 45 '-' 89 17]}}   % affiche 4176 = (13+45)*(89-17)
   {Browse {EvalPrefix ['-' '*' '+' 13 45 89 17]}}   % affiche 5145 = ((13+45)*89)-17
   {Browse {EvalPrefix ['*' 13 '+' 45 '-' 89 17]}}   % affiche 1521 = 13*(45+(89-17))
```
Solution. Commençons par définir une abstraction de données pour la pile. Les opérations sont relativement évidentes.
```
   fun {NewStack} {NewCell nil} end
   fun {IsEmpty S} @S==nil end
   proc {Push S X} S:=X|@S end
   fun {Pop S} case @S of X|T then S:=T X end end
```
Avant d'implémenter l'algorithme, nous allons définir deux fonctions pour manipuler les opérateurs. La fonction IsOperator renvoie true si son argument est un opérateur, false sinon. Elle réutilise la fonction Member définie sur les listes. La fonction ApplyOperator permet d'appliquer un opérateur sur deux opérandes données. Notez que ces deux fonctions définissent un type abstrait opérateur...
```
   %% renvoie true si X est un operateur
   fun {IsOperator X}
      {Member X ['+' '-' '*' '/']}
   end

   %% applique Op sur X et Y et renvoie le resultat
   fun {ApplyOperator Op X Y}
      case Op
      of '+' then X+Y
      [] '-' then X-Y
      [] '*' then X*Y
      [] '/' then X div Y
      end
   end
```
Voici maintenant une implémentation de l'algorithme d'évaluation. La fonction EvalPrefix crée une pile S et définit une fonction et une procédure auxiliaires qui utilisent la pile. La fonction Eval lit le premier élément de la liste restante Ys et met la pile à jour. La procédure TreatValue applique itérativement les opérateurs nécessaires sur son argument.
```
   %% renvoie l'evaluation de l'expression prefixe Xs
   fun {EvalPrefix Xs}
      S={NewStack}

      %% evalue le reste de l'expression Ys
      fun {Eval Ys}
         case Ys
         of nil then {Pop S}
         [] Y|Yr andthen {IsOperator Y} then {Push S Y} {Eval Yr}
         [] Y|Yr then {TreatValue Y} {Eval Yr}
         end
      end

      %% traite la valeur Y en appliquant les operateurs necessaires
      proc {TreatValue Y}
         if {IsEmpty S} then {Push S Y} else
            X={Pop S} in
            if {IsOperator X} then   % Y est la premiere operande de X
               {Push S X} {Push S Y}
            else   % X et Y sont les operandes de Op
               Op={Pop S} in {TreatValue {ApplyOperator Op X Y}}
            end
         end
      end
   in
      {Eval Xs}
   end
```

Collections et ensembles. Cet exercice est une variante de l'exercice Collections de la séance 11. On reprend la classe Collection, qui définit les trois méthodes put(X), get(X) et isEmpty(B).

   class Collection
      attr elements
      meth init   % initialise la collection
         elements:=nil
      end
      meth put(X)   % insère X
         elements:=X|@elements
      end
      meth get($)   % extrait un élément et le renvoie
         case @elements of X|Xr then elements:=Xr X end
      end
      meth isEmpty($)   % renvoie true ssi la collection est vide
         @elements==nil
      end
   end

Ajoutez à cette classe une méthode qui permet de tester si une valeur est présente dans la collection. Si C est une collection, l'appel {C member(X $)} renvoie true si X est dans la collection C, false sinon. Votre méthode peut utiliser l'implémentation de la classe Collection.
Dans une collection, un élément peut apparaître plusieurs fois. Les ensembles sont définis comme des collections où tout élément apparaît au plus une fois. Définissez une classe Set pour des ensembles. Votre classe doit hériter de la classe Collection, mais elle ne peut pas dépendre de son implémentation.

Solution. Commençons par compléter la classe Collection en définissant la méthode member. Il suffit pour cela d'utiliser la fonction Member définie sur les listes.

   class Collection
      attr elements
      meth init   % initialise la collection
         elements:=nil
      end
      meth put(X)   % insère X
         elements:=X|@elements
      end
      meth get($)   % extrait un élément et le renvoie
         case @elements of X|Xr then elements:=Xr X end
      end
      meth isEmpty($)   % renvoie true ssi la collection est vide
         @elements==nil
      end
      meth member(X $)   % renvoie true ssi X est dans la collection
         {Member X @elements}
      end
   end

Nous pouvons maintenant définir la classe Set. Comme nous héritons de la classe Collection, toutes les méthodes de Collection sont réutilisables. L'idée est simple. Nous allons surcharger la méthode put de sorte qu'un élément n'est inséré que s'il n'est pas déjà présent dans l'ensemble. Pour voir si l'élément est présent, on utilise la méthode member dont on a hérité. Pour insérer effectivement l'élément, on doit appeler la méthode put de la classe Collection.

   class Set from Collection
      meth put(X)
         if {self member(X $)} then
            skip                % X est deja dans l'ensemble
         else
            Collection,put(X)   % insere X en appelant la methode heritee
         end
      end
   end

Vérifions la propriété avec un exemple. Nous construisons un ensemble E en y insérant plusieurs fois le même élément. Ensuite, on enlève tous les éléments de l'ensemble et on les renvoie dans une liste. On vérifie alors si un élément apparaît plusieurs fois dans la liste.

   declare
   E={New Set init}
   {E put(1)}
   {E put(2)}
   {E put(3)}
   {E put(1)}   % l'element 1 est insere deux fois

   local
      %% vide l'ensemble S et renvoie la liste de ses elements
      fun {GetElements S}
         if {S isEmpty($)} then nil else
            {S get($)}|{GetElements S}
         end
      end
   in
      {Browse {GetElements E}}   % l'element 1 apparait une seule fois
   end

Raphaël Collet - 8 décembre 2005

`* + 13 45 - 89 17`	`+ 13 45 - 89 17`	`13 45 - 89 17`	`45 - 89 17`	`58 - 89 17`	`- 89 17`	`89 17`	`17`	`72`	`4176`
	`*`	`+ *`	`13 + *`	`*`	`58 *`	`- 58 *`	`89 - 58 *`	`58 *`		`4176`